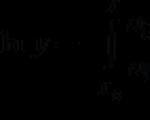Моделирование случайных событий. Случайные величины дискретного типа и формулы для их разыгрывания Процедура поиска в глубину

Обозначим равномерно распределенную СВ в интервале (0, 1) через R, а ее возможные значения (случайные числа) - r j .

Разобьем интервал . Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность = 0,85 (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем равно 1,05 час.

Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме: P 0 , P 1 , P 2 , P 3 , P 4 , P отк, q,A, L оч, L сис, T оч, T сис

ЗАНЯТИЕ 4

Многоканальные СМО с ожиданием, с ожиданием и ограниченной длиной очереди

Рассмотрим многоканальную систему массового обслуживания с ожиданием. Данный тип СМО часто используется при моделировании групп абонентских терминалов ЛВС, работающих в диалоговом режиме. Процесс массового обслуживания при этом характеризуется следующим: входной и выходной потоки являются пуассоновскими с интенсивностями и соответственно; параллельно обслуживаться могут не более n клиентов. Система имеет n каналов обслуживания. Средняя продолжительность обслуживания одного клиента равна 1/м для каждого канала. Эта система также относится к процессу гибели и размножения.

с=л/nм - отношение интенсивности входящего потока к суммарной интенсивности обслуживания, является коэффициентом загрузки системы

(с<1). Существует стационарное распределение числа запросов в рассматриваемой системе. При этом вероятности состояний Р к определяются:

где Р 0 - вероятность свободного состояния всех каналов при неограниченной очереди, k-количество заявок.

если принять с=л / м, то Р 0 можно определить для неограниченной очереди:

Для ограниченной очереди:

где m-длина очереди

При неограниченной очереди:

Относительная пропускная способность q=1,

Абсолютная пропускная способность А=л,

Среднее число занятых каналов Z=А/м

При ограниченной очереди

1 Межузловая ветвь вторичной сети связи имеет n = 4 каналов. Поток сообщений, поступающих для передачи по каналам ветви связи, имеет интенсивность = 8 сообщений в секунду. Среднее время t = 0,1 передачи одного сообщения каждым каналом связи равно t/n = 0,025 секунд. Время ожидания сообщений в очереди неограниченно. Найти характеристики СМО:

Р отк - вероятность отказа передачи сообщений;

Q - относительную пропускную способность ветви связи;

А - абсолютную пропускную способность ветви связи;

Z - среднее число занятых каналов;

L оч - среднее число сообщений в очереди;

Т ож - среднее время ожидания;

Т сист - среднее суммарное время пребывания сообщений в очереди и передачи по ветви связи.

2. Механическая мастерская завода с тремя постами (каналами) выполняет ремонт малой механизации. Поток неисправных механизмов, прибывающих в мастерскую, - пуассоновский и имеет интенсивность = 2,5 механизма в сутки, среднее время ремонта одного механизма распределено по показательном у закону и равно = 0,5 сут. Предположим, что другой мастерской на заводе нет, и, значит, очередь механизмов перед мастерской может расти практически неограниченно. Требуется вычислить следующие предельные значения вероятностных характеристик системы:

Вероятности состояний системы;

Среднее число заявок в очереди на обслуживание;

Среднее число находящихся в системе заявок;

Среднюю продолжительность пребывания заявки в очереди;

Среднюю продолжительность пребывания заявки в системе.

3. Межузловая ветвь вторичной сети связи имеет n=3 канала. Поток сообщений, поступающих для передачи по каналам ветви связи, имеет интенсивность л=5 сообщений в секунду. Среднее время передачи одного сообщения t=0,1 , t/n=0,033 сек.. В накопителе очереди ожидающих передачи сообщений может находиться до m= 2 сообщений. Сообщение, прибывшее в момент, когда все места в очереди заняты, получает отказ передачи по ветви связи. Найти характеристики СМО: Р отк -вероятность отказа передачи сообщений, Q-относительную пропускную способность, А- абсолютную пропускную способность, Z- среднее число занятых каналов, L оч - среднее число сообщений в очереди, Т ож - среднее время ожидания, Т сист - среднее суммарное время пребывания сообщения в очереди и его передачи по ветви связи.

ЗАНЯТИЕ 5

Замкнутая СМО

Рассмотрим модель обслуживания машинного парка, которая представляет собой модель замкнутой системы массового обслуживания. До сих пор мы рассматривали только такие системы массового обслуживания, для которых интенсивность входящего потока заявок не зависит от состояния системы. В этом случае источник заявок является внешним по отношению к СМО и генерирует неограниченный поток требований. Рассмотрим системы массового обслуживания, для которых зависит от состояния системы, при чем источник требований является внутренним и генерирует ограниченный поток заявок. Например, обслуживается машинный парк, состоящий из N машин, бригадой R механиков (N > R), причем каждая машина может обслуживаться только одним механиком. Здесь машины являются источниками требований (заявок на обслуживание), а механики - обслуживающими каналами. Неисправная машина после обслуживания используется по своему прямому назначению и становится потенциальным источником возникновения требований на обслуживание. Очевидно, что интенсивность зависит от того, сколько машин в данный момент находится в эксплуатации (N - k) и сколько машин обслуживается или стоит в очереди, ожидая обслуживания (k). В рассматриваемой модели емкость источника требований следует считать ограниченной. Входящий поток требований исходит из ограниченного числа эксплуатируемых машин (N - k), которые в случайные моменты времени выходят из строя и требуют обслуживания. При этом каждая машина из (N - k) находится в эксплуатации. Генерирует пуассоновский поток требований с интенсивностью X независимо от других объектов, общий (суммарный) входящий поток имеет интенсивность. Требование, поступившее в систему в момент, когда свободен хотя бы один канал, немедленно идет на обслуживание. Если требование застает все каналы занятыми обслуживанием других требований, то оно не покидает систему, а становится в очередь и ждет, пока один из каналов не станет свободным. Таким образом, в замкнутой системе массового обслуживания входящий поток требований формируется из выходящего. Состояние S k системы характеризуется общим числом требований, находящихся на обслуживании и в очереди, равным k. Для рассматриваемой замкнутой системы, очевидно, k = 0, 1, 2, ... , N. При этом если система находится в состоянии S k , то число объектов, находящихся в эксплуатации, равно (N - k). Если - интенсивность потока требований в расчете на одну машину, то:

Система алгебраических уравнений, описывающих работу замкнутой СМО в стационарном режиме, выглядит следующим образом:

Решая данную систему, находим вероятность k-гo состояния:

Величина P 0 определяется из условия нормирования полученных результатов по формулам для P k , k = 0, 1, 2, ... , N. Определим следующие вероятностные характеристики системы:

Среднее число требований в очереди на обслуживание:

Среднее число требований, находящихся в системе (на обслуживании и в очереди)

среднее число механиков (каналов), «простаивающих» из-за отсутствия работы

Коэффициент простоя обслуживаемого объекта (машины) в очереди

Коэффициент использования объектов (машин)

Коэффициент простоя обслуживающих каналов (механиков)

Среднее время ожидания обслуживания (время ожидания обслуживания в очереди)

Задача по замкнутой СМО

1. Пусть для обслуживания десяти персональных компьютеров (ПК) выделено два инженера одинаковой производительности. Поток отказов (неисправностей) одного компьютера - пуассоновский с интенсивностью = 0,2. Время обслуживания ПК подчиняется показательному закону. Среднее время обслуживания одного ПК одним инженером составляет: =1,25 час. Возможны следующие варианты организации обслуживания:

Оба инженера обслуживают все десять компьютеров, так что при отказе ПК его обслуживает один из свободных инженеров, в этом случае R = 2, N = 10;

Каждый из двух инженеров обслуживает по пять закрепленных за ним ПК. В этом случае R = 1, N = 5.

Необходимо выбрать наилучший вариант организации обслуживания ПК.

Надо опр-ть все вероятности состояний Р к: Р 1 - Р 10 , учитывая, что и используя результаты расчета Р к, вычислим Р 0

ЗАНЯТИЕ 6

Вычисление трафика.

Теория телетрафика - раздел теории массового обслуживания. Основы теории телетрафика заложил датский ученый А.К. Эрланг. Его работы были опубликованы в 1909-1928 гг. Дадим важные определения, используемые в теории телетрафика (ТТ). Термин «трафик» (англ.,traffic) соответствует термину «телефонная нагрузка». Подразумевается нагрузка, создаваемая потоком вызовов, требований, сообщений, поступающих на входы СМО. Объемом трафика называют пропущенную тем или иным ресурсом величину суммарного, интегрального интервала времени, в течение которого данный ресурс был занят за анализируемый период времени. Единицей работы можно считать секундозанятие ресурса. Иногда можно прочитать о часозанятии, а порой и просто - секундах или часах. Однако рекомендации ITU дают размерность объема трафика в эрлангочасах. Чтобы понять смысл такой единицы измерения, надо рассмотреть еще один параметр трафика - интенсивность трафика. При этом чаще говорят о средней интенсивности трафика (нагрузки) на некотором заданном пуле (наборе) ресурсов. Если в каждый момент времени t из заданного интервала (t 1 ,t 2) число занятых обслуживанием трафика ресурсов из данного набора равно А(t), то средняя интенсивность трафика будет

Величина интенсивности трафика характеризуется как среднее число ресурсов, занятых обслуживанием трафика на заданном интервале времени. Единицей измерения интенсивности нагрузки является один Эрланг (1 Эрл, 1 Е)., т.е. 1 эрланг- это такая интенсивность трафика, которая требует полной занятости одного ресурса, или, иначе говоря, при которой ресурсом выполняется работа величиной в одно секундо-занятие за время в одну секунду. В американской литературе иногда можно встретить другую единицу измерения, называемую CCS- Centrum (or hundred) Calls Second (гектосекундозанятия). Число CCS отражает время занятия серверов в 100 секундных интервалов за 1 час. Интенсивность, измеренную в CCS, можно пересчитать в Эрланги по формуле 36CCS=1 Эрл.

Трафик, создаваемый одним источником и выраженный в часо-занятиях, равен произведению числа попыток вызовов с за определенный интервал времени Т на среднюю длительность одной попытки t: у = с t (ч-з). Трафик можно вычислить тремя разными способами:

1) пусть число вызовов с в течение часа равно 1800, а средняя длительность занятия t = 3 мин, тогда Y = 1800 выз. /ч. 0,05 ч = 90 Эрл;

2) пусть в течение времени Т фиксируются длительности t i всех n занятий выходов некоторого пучка, тогда трафик определяют так:

3) пусть в течение времени Т выполняется наблюдение через равные промежутки времени за количеством одновременно занятых выходов некоторого пучка, по результатам наблюдений строят (рисунок 8) ступенчатую функцию времени x(t).

Рисунок 8. Отсчеты одновременно занятых выходов пучка

Трафик в течение времени Т может быть оценен как среднее значение х(t) за это время:

где n - число отсчетов одновременно занятых выходов. Величина Y есть среднее количество одновременно занятых выходов пучка в течение времени Т.

Колебания трафика. Трафик вторичных телефонных сетей существенно колеблется во времени. В течение рабочего дня кривая трафика имеет два или даже три пика (рисунок 9).

Рисунок 9. Колебания трафика в течение суток

Час суток, в течение которого трафик, наблюдаемый длительное время, имеет наибольшее значение, называют часом наибольшей нагрузки (ЧНН). Знание трафика в ЧНН принципиально важно, так как им определяется количество каналов (линий), объем оборудования станций и узлов. Трафик одного и того же дня недели имеет сезонные колебания. Если день недели является предпраздничным, то ЧНН этого дня выше, чем и день после праздника. Если количество служб, поддерживаемых сетью, растет, то и трафик растет. Поэтому проблематично предсказывать с достаточной уверенностью возникновение пиков трафика. Трафик внимательно отслеживается администрацией сетей и проектными организациями. Правила измерения трафика разработаны МСЭ-Т и используются администрациями национальных сетей для того, чтобы удовлетворить требованиям качества предоставляемых услуг, как для абонентов своей сети, так и для абонентов других сетей, связанных с ней. Теорию телетрафика можно использовать для практических расчетов потерь или объема оборудования станции (узла) только в том случае, если трафик стационарный (статистически установившийся). Этому условию приближенно удовлетворяет трафик в ЧНН. Величина нагрузки, поступающая за сутки на АТС, влияет на профилактику и ремонт оборудования. Неравномерность поступления нагрузки на станцию в течение суток определяется коэффициентом концентрации

Более строго определение ЧНН производится следующим образом. Рекомендация ITU Е.500 предписывает проанализировать данные об интенсивности за 12 месяцев, выбрать из них 30 наиболее загруженных дней, найти в эти дни наиболее загруженные часы и усреднить результаты измерения интенсивности на этих интервалах. Такой расчет интенсивности трафика (нагрузки) называют нормальной оценкой интенсивности трафика в ЧНН или уровнем А. более жесткой оценки можно проводить усреднение за 5 самых загруженных дней выбранного 30-дневного периода. Такая оценка носит название повышенной или оценкой по уровню В.

Процесс создания трафика. Как известно каждому пользователю телефонной сети, не все попытки установления соединения с вызываемым абонентом заканчиваются успешно. Иногда приходится делать несколько неудачных попыток, прежде чем будет установлено желаемое соединение.

Рисунок 10. Диаграмма событий при установлении соединения между абонентами

Рассмотрим возможные события при моделировании установления соединения между абонентами А и Б (рисунок 10). Статистические данные о вызовах в телефонных сетях таковы: доля состоявшихся разговоров составляет 70-50 %, доля несостоявшихся - 30-50 %. Любая попытка абонента занимает вход СМО. При удачных попытках (когда разговор состоялся) время занятия коммутационных приборов, устанавливающих соединения входов с выходами, больше, чем при неудачных попытках. Абонент может в любой момент времени прервать попытки установления соединения. Повторные попытки могут быть вызваны следующими причинами:

Номер набран неправильно;

Предположение об ошибке в работе сети;

Степень срочности разговора;

Неудачные предыдущие попытки;

Знание привычек абонента Б;

Сомнение в правильности набора номера.

Повторная попытка может быть предпринята в зависимости от следующих обстоятельств:

Степени срочности;

Оценки причины неуспеха;

Оценки целесообразности повторения попыток,

Оценки приемлемого интервала между попытками.

Отказ от повторной попытки может быть связан с низкой степенью срочности. Различают несколько видов трафика, создаваемого вызовами: поступающий (предложенный) Y п и пропущенный Y пр. Трафик Y п включает все успешные и неуспешные попытки, трафик У пр, являющийся частью Y п, включает успешные и часть неуспешных попыток:

Y пр = Y р + Y нп,

где Y р - разговорный (полезный) трафик, а Y нп - трафик, созданный неудачными попытками. Равенство Y п = Y р возможно лишь в том идеальном случае, если нет потерь, ошибок вызывающих абонентов и не ответов вызываемых абонентов.

Разность между поступающей и пропущенной нагрузками за определенный промежуток времени будет являться потерянной нагрузкой.

Прогнозирование трафика. Ограниченность ресурсов приводит к необходимости поэтапного расширения станции и сети. Администрация сети делает прогноз увеличения трафика в течение этапа развития, учитывая, что:

Доход определяется частью пропущенного трафика Y р, - затраты определяются качеством обслуживания при наибольшем трафике;

Большая доля потерь (низкое качество) бывает в редких случаях и характерна для конца периода развития;

Наибольший объем пропущенного трафика приходится на периоды, когда потери практически отсутствуют, - если потери меньше 10 %, то абоненты на них не реагируют. При планировании развития станций и сети проектировщик должен ответить на вопрос, каковы требования к качеству предоставления услуг (к потерям). Для этого нужно проводить измерения трафика потерь по принятым в стране правилам.

Пример измерения трафика.

Сначала рассмотрим, как можно отображать работу СМО, имеющую несколько ресурсов, которые одновременно обслуживают некоторый трафик. Будем далее говорить о таких ресурсах, как о серверах, которые обслуживают поток заявок или требований. Одним из наиболее наглядных и часто употребляемых способов изображения процесса обслуживания заявок пулом серверов является диаграмма Ганта (Gantt). Эта диаграмма представляет собой прямоугольную систему координат, ось абсцисс которой изображает время, а на оси ординат помечаются дискретные точки, соответствующие серверам пула. На рисунке 11 изображена диаграмма Ганта для системы с тремя серверами.

В первые три интервала времени (считаем их секундой) заняты первый и третий серверы, следующие две секунды - только третий, затем одну секунду работает второй, потом, две секунды второй и первый, и последние две секунды- только первый.

Построенная диаграмма позволяет произвести расчеты объема трафика и его интенсивности. Диаграмма отражает только обслуженный или пропущенный трафик, поскольку ничего не говорит о том, поступали ли в систему заявки, которые не смогли быть обслужены серверами.

Объем пропущенного трафика вычисляется как суммарная длина всех отрезков диаграммы Ганта. Объем за время 10 секунд:

Свяжем с каждым временным интервалом отложенным по оси абсцисс, целое число, равное количеству серверов, занятых на этом единичном интервале. Эта величина А(t) - мгновенная интенсивность. Для нашего примера

А(t)= (2, 2, 2, 1, 1, 1, 2, 2, 1, 1)

Найдем теперь среднюю за период 10 секунд интенсивность трафика

Таким образом, средняя интенсивность трафика, пропущенного рассматриваемой системой из трех серверов, равна 1,5 Эрл.

Основные параметры нагрузки

Телефонной связью пользуются различные категории абонентов, которые характеризуются:

числом источников нагрузки- N,

средним числом вызовов от одного источника за определенное время (ЧНН обычно)- c,

средней длительностью одного занятия коммутационной системы при обслуживании одного вызова- t.

Величина интенсивности нагрузки будет

Определим различные источники вызовов. Например,

Среднее число вызовов в ЧНН от одного учрежденческого аппарата;

Среднее число вызовов от одного квартирного индивидуального аппарата; случайное событие массовое обслуживание телетрафик

с кол - то же от аппарата коллективного пользования;

с ма - то же от одного монетного аппарата;

с сл - то же от одной соединительной линии.

Тогда среднее число вызовов от одного источника:

Существуют приблизительные данные для среднего числа вызовов от одного источника соответствующей категории:

3,5 - 5, =0,5 - 1, с кол = 1,5 - 2, с ма =15 - 30, с сл =10 - 30.

Различают следующие виды соединений, которые в зависимости от исхода соединения создают на станции различную по величине телефонную нагрузку:

k р - коэффициент, показывающий долю соединений, окончившихся разговором;

k з - соединения, не окончившиеся разговором из-за занятости вызываемого абонента;

k но - коэффициент, выражающий долю соединений, не окончившихся разговором по причине неответа вызываемого абонента;

k ош - соединения, не окончившиеся разговором из-за ошибок вызывающего абонента;

k тех - вызовы, не окончившиеся разговором по техническим причинам.

При нормальной работе сети значения этих коэффициентов равны:

k р =0,60-0,75; k з =0,12-0,15; k но =0,08-0,12; k ош =0,02-0,05; k тех =0,005-0,01.

Средняя длительность занятия зависит от видов соединений. Например, если соединение закончилось разговором, средняя длительность занятия приборов t сост будет равна

где - длительность установления соединения;

t сост. - состоявшийся разговор;

t в - длительность посылки вызова в телефонный аппарат вызываемого абонента;

t р - длительность разговора

где t со - сигнал ответа станции;

1,5n- время набора номера вызываемого абонента (n-количество знаков в номере);

t с - время, необходимое для установления соединения коммутационными механизмами и разъединения соединения после окончания разговора. Примерные значения рассмотренных величин:

t со =3сек., t c = 1-2,5сек., t в = 8-10сек., t р =90-130сек.

Вызовы, не окончившиеся разговором тоже создают телефонную нагрузку.

Среднее время занятия приборов при занятости вызываемого абонента равна

где t уст.соед. определяется по (4.2.3)

t зз - время слушания зуммера занятости, t зз =6сек.

Средняя длительность занятия приборов при не ответе вызываемого абонента равна

где t пв - время слушания сигнала контроля посылки вызова, t пв =20сек.

Если разговора не было из-за ошибок абонента, то в среднем t ош =30 сек.

Длительность занятий, не окончившихся разговором по техническим причинам, не определена, так как процент таких занятий мал.

Из всего выше сказанного следует, что полная нагрузка, создаваемая группой источников за ЧНН, равна сумме нагрузок отдельных видов занятий.

где - коэффициент, учитывающий слагаемые как доли

На телефонной сети с семизначной нумерацией запроектирована АТС, структурный состав абонентов которой следующий:

N учр =4000, Nинд=1000, N кол =2000, N ма =400, N сл =400.

Среднее число вызовов, поступающее от одного источника в ЧНН, равно

По формулам (4.2.3) и (4.2.6) находим нагрузку

1.10.62826767 сек.зан.=785,2чз.

Средняя длительность занятия t из формулы Y=Nct

t= Y/Nc= 2826767/7800*3.8=95.4 сек.

Задача на нагрузку

1.На телефонной сети с семизначной нумерацией запроектирована АТС, структурный состав абонентов которой следующий:

N учр =5000, Nинд=1500, N кол =3000, N ма =500, N сл =500.

Определить нагрузку, поступающую на станцию - Y, среднюю длительность занятия t, если известно, что

с учр =4, с инд =1, с кол =2, с ма =10, с сл =12, t р =120 сек., t в =10 сек., k р =0,6, t с =1 сек., =1,1.

Размещено на Allbest.ru

Подобные документы

Понятие равномерно распределенной случайной величины. Мультипликативный конгруэнтный метод. Моделирование непрерывных случайных величин и дискретных распределений. Алгоритм имитационного моделирования экономических отношений между кредитором и заемщиком.

курсовая работа , добавлен 03.01.2011


Общие понятия теории массового обслуживания. Особенности моделирования систем массового обслуживания. Графы состояний СМО, уравнения, их описывающие. Общая характеристика разновидностей моделей. Анализ системы массового обслуживания супермаркета.

курсовая работа , добавлен 17.11.2009


Элементы теории массового обслуживания. Математическое моделирование систем массового обслуживания, их классификация. Имитационное моделирование систем массового обслуживания. Практическое применение теории, решение задачи математическими методами.

курсовая работа , добавлен 04.05.2011


Понятие случайного процесса. Задачи теории массового обслуживания. Классификация систем массового обслуживания (СМО). Вероятностная математическая модель. Влияние случайных факторов на поведение объекта. Одноканальная и многоканальная СМО с ожиданием.

курсовая работа , добавлен 25.09.2014


Изучение теоретических аспектов эффективного построения и функционирования системы массового обслуживания, ее основные элементы, классификация, характеристика и эффективность функционирования. Моделирование системы массового обслуживания на языке GPSS.

курсовая работа , добавлен 24.09.2010


Разработка теории динамического программирования, сетевого планирования и управления изготовлением продукта. Составляющие части теории игр в задачах моделирования экономических процессов. Элементы практического применения теории массового обслуживания.

практическая работа , добавлен 08.01.2011


Элементарные понятия о случайных событиях, величинах и функциях. Числовые характеристики случайных величин. Виды асимметрии распределений. Статистическая оценка распределения случайных величин. Решение задач структурно-параметрической идентификации.

курсовая работа , добавлен 06.03.2012


Моделирование процесса массового обслуживания. Разнотипные каналы массового обслуживания. Решение одноканальной модели массового обслуживания с отказами. Плотность распределения длительностей обслуживания. Определение абсолютной пропускной способности.

контрольная работа , добавлен 15.03.2016


Функциональные характеристики системы массового обслуживания в сфере автомобильного транспорта, ее структура и основные элементы. Количественные показатели качества функционирования системы массового обслуживания, порядок и главные этапы их определения.

лабораторная работа , добавлен 11.03.2011


Постановка цели моделирования. Идентификация реальных объектов. Выбор вида моделей, математической схемы. Построение непрерывно-стахостической модели. Основные понятия теории массового обслуживания. Определение потока событий. Постановка алгоритмов.

Напомним предварительно, что если случайная величина R распределена равномерно в интервале (0,1), то ее математическое ожидание и дисперсия соответственно равны (см. гл. XII, § 1, замечание 3):

M (R )= 1/2, (*)

D (R )= 1/2. (**)

Составим сумму п независимых, распределенных рав­номерно в интервале (0,1) случайных величин R j (j =1, 2, ...,n):

Для нормирования этой суммы найдем предварительно ее математическое ожидание и дисперсию.

Известно, что математическое ожидание суммы слу­чайных величин равно сумме математических ожиданий слагаемых. Сумма (***) содержит п слагаемых, матема­тическое ожидание каждого из которых в силу (*) равно 1/2; следовательно, математическое ожидание суммы (*** )

Известно, что дисперсия суммы независимых случай­ных величин равна сумме дисперсий слагаемых. Сумма (***) содержит n независимых слагаемых, дисперсия каж­дого из которых в силу (**) равна 1/12; следовательно, дисперсия суммы (***)

Отсюда среднее квадратическое отклонение суммы (***)

Пронормируем рассматриваемую сумму, для чего выч­тем математическое ожидание и разделим результат на среднее квадратическое отклонение:

В силу центральной предельной теоремы при п→∞ распределение этой нормированной случайной величины стремится к нормальному с параметрами а= 0 и σ=1. При конечном п распределение прибли­женно нормальное. В частности, при п = 12 получим достаточно хорошее и удобное для расчета приближение

Правило. Для того чтобы разыграть возможное зна­чение x i нормальной случайной величины Х с парамет­рами а=0 и σ=1, надо сложить 12 независимых слу­чайных чисел и из полученной суммы вычесть 6:

Пример, а) Разыграть 100 возможных значений нормальной вели­чины Х с параметрами а=0 и σ=1; б) оценить параметры разыг­ранной величины.

Решение. а) Выберем 12 случайных чисел из первой строки таблицы *) , сложимих и из полученной суммы вычтем 6; в итоге имеем

x i =(0,10+0,09+...+0,67) - 6= - 0,99.

Аналогично, выбирая из каждой следующей строки таблицы пер­вые 12 чисел, найдем остальные возможные значения X.

б) Выполнив расчеты, получим искомые оценки:

Оценки удовлетворительные: а* близко к нулю, σ* мало отличается от единицы.

Замечание. Если требуется разыграть возможное значение z i , нормальной случайной величины Z с математическим ожиданием а и средним квадратическим отклонением σ , то, разыграв по пра­вилу настоящего параграфа возможное значение x i , находят искомое возможное значение по формуле

z i =σx i +a.

Эта формула получена из соотношения (z i -a )/σ=x i .

Задачи

1. Разыграть 6 значений дискретной случайной величины X, закон распределения которой задан в виде таблицы

X		3,2
p	0,18	0,24	0,58

Указание. Для определенности принять, что выбраны слу­чайные числа: 0,73; 0,75; 0,54; 0,08; 0,28; 0,53. Отв. 10; 10; 10; 2; 3; 22; 10.

2. Разыграть 4 испытания, в каждом из которых вероятность появления события А равна 0,52.

Указание. Для определенности принять, что выбраны слу­чайные числа: 0;28; 0,53; 0,91; 0,89.

Отв. А, , .

3. Заданы вероятности трех событий, образующих полную группу: Р (А 1)=0,20, Р (А 2)=0,32, Р (А 3 )= 0,48. Разыграть 6 испытаний, в каждом из которых появляется одно из заданных событий.

Указание. Для определенности принять, что выбраны слу­чайные числа: 0,77; 0,19; 0,21; 0,51; 0,99; 0,33.

Отв. А 3 , А 1 , А 2 , А 2 , А 3 , А 2 .

4. События А и В независимы и совместны. Разыграть 5 испы­таний, в каждом из которых вероятность появления события А равна 0,5, а события В- 0,8.

А 1 =АВ , для определенности принять случайные числа: 0,34; 0,41; 0,48; 0,21; 0,57.

Отв. А 1 , А 2 , А 2 , А 1 , А 3 .

5. События А, В, С независимы и совместны. Разыграть 4 испы­тания в каждом из которых вероятности появления событий заданы: Р (А )= 0,4, Р (В )= 0,6, Р (С )= 0,5.

Указание. Составить полную группу событий: для определенности принять, что выбраны случайные числа: 0,075; 0,907; 0,401; 0,344.

Отв.А 1 , А 8 , А 4 , А 4 .

6. События А и В зависимы и совместны. Разыграть 4 испытания, в каждом из которых заданы вероятности: Р (А )=0,7, Р (В )=0,6, Р (АВ )=0,4.

Указание. Составить полную группу событий: А 1 =АВ , для определенности принять случайные числа: 0,28; 0,53; 0,91; 0,89.

Отв. А 1 , А 2 , А 4 , А 3 .

7. Разыграть 3 возможных значения непрерывной случайной величины X, которая распределена по показательному закону и задана функцией распределения F (х )= 1 - е -10 x .

Указание. Для определенности принять, что выбраны слу­чайные числа: 0,67; 0,79; 0,91.

Отв. 0,04; 0,02; 0,009.

8. Разыграть 4 возможных значения непрерывной случайной величины X, распределенной равномерно в интервале (6,14).

Указание. Для определенности принять, что выбраны слу­чайные числа: 0,11: 0,04; 0,61; 0,93.

Отв. 6,88; 6,32; 10,88; 13,44.

9. Найти методом суперпозиции явные формулы для разыгрывания непрерывной случайной величины X, заданной функцией рас­пределения

F (x )=1- (1/3)(2е- 2 x +е -3 x:), 0<х <∞.

Отв. х= - (1/2)1п r 2 , если r 1 < 2/3; х = - (1/3)1п r 2 , если r 1 ≥2/3.

10. Найти явную формулу для разыгрывания непрерывной слу­чайной величины X, заданной плотностью вероятности f (х )=b /(1 +ax ) 2 в интервале 0≤x ≤1/(b-a ); вне этого интервала f(x)=0.

Отв. х i = - r i /(b - ar i ).

11. Разыграть 2 возможных значения нормальной случайной величины с параметрами: а) а =0, σ =1; б) а =2, σ =3.

Указание. Для определенности принять случайные числа (далее указано число сотых долей; например, числу 74 соответствует слу­чайное число r 1 =0,74): 74. 10, 88, 82. 22, 88, 57, 07, 40, 15, 25, 70; 62, 88, 08, 78, 73, 95, 16, 05, 92, 21, 22, 30.

Отв. а) x 1 = - 0,22, x 2 = - 0.10; 6) z 1 =1,34, z 2 =2,70.

Глава двадцать вторая

Пусть, например, перед нами поставлена задача получить ряд значений дискретной случайной величины X с распределением

где – возможные значения случайной величины Х , расположенные в убывающем порядке; – вероятности этих значений,

Для решения этой задачи представим себе (см. пример в начале главы), что единичный квадрат, площадь которого S o =l, разделен на k площадок, размеры которых S 1 , S 2 ,… , S k заданы в долях единицы и равны соответственно вероятностям p 1 , p 2 , ..., p k . Выберем в единичном квадрате N случайных, равномерно распределенных точек, каждая из которых задана координатами (х, у), представляющими собой значения случайных величин X и Y, равномерно распределенных в интервале от 0 до 1 .

Если i -я точка (i = 1, 2, ..., N) попала в какую-то j -ю площадку, то будем считать, что мы получили значение X, равное , т. е. х i = ξ j . Если i+1 -я точка попала в какую-то ζ - ю площадку, то будем считать, что мы получили значение X, равное ξ j , т. е. х i +1 = ξ j . И так далее.

В пределе при достаточно большом N распределение полученных значений X (х 1 , х 2 ,… , x n) будет сходиться по вероятности к заданному распределению. Это с очевидностью сле­дует из того, что вследствие равномерного распределения случайных точек в площади единичного квадрата число попаданий в каждую площадку при N → ∞ со будет определяться ее размерами, в свою очередь равными вероятности j -го значения случайной величины.

В данном случае двумерные координаты (х, у) использовались только для уяснения аналогии и общности алгоритма метода Монте-Карло при решении различных задач. Вообще же для решения задачи розыгрыша дискретной случайной величины достаточно иметь одну числовую ось.

Подготовка к розыгрышу при этом заключается в том, что на числовой оси У (рис. 9.2) откладывается интервал от 0 до 1 , (), который разбивается, начиная от нуля, на k интервалов длиной, равной соответственно p 1 , p 2 , . . ., p k . Полученные интервалы нумеруются цифрами j = 1, 2, 3, . .., k.

Сам розыгрыш заключается в следующем. Каким-либо способом, например из таблицы случайных чисел, равномерно распределенных(см.

Рисунок 9.2. Вероятности значений случайной величины на числовой оси

разд. 9.4) в интервале от 0 до 1, последовательно считываются значения a i . (i = 1, 2, ... , N) . Затем на оси У определяется в какой интервал на оси У попадает заданное значение точки, то есть где у j = a i .

Если точка а i попадает в интервал с номером j , то считается, что данное значение х i = ξ j . , и т. д.

Разыгрывание дискретной случайной величины, состоящее из множества испытаний, обычно производится на ЭВМ. При этом значения случайной величины а могут быть получены различными путями (см. разд. 9.4).

Пусть распределение разыгрываемой случайной величины задано в памяти машины в виде табл. 9.1.

Таблица 9.1

Распределение дискретной случайной величины

Значения X	ζ 1	ζ 2	…	ζ i	…	ζ к
Вероятность значений	p 1	p 2	…	p i	…	p k
Обеспеченность	P 1	P 2	…	P i	…	P k

В этой таблице i - порядковый номер значений случайной ве­личины X; - значения случайной величины, расположенные в убывающем порядке; р i - вероятность значений ; - обеспеченность значений .

Разыгрывание производится по следующей схеме (рис. 9.3). Задается номер члена ряда (i =1, 2, ..., п). Затем по таблице случайных чисел находится a i , дальше a j сравнивается со значениями обеспеченности Р j (j = 1, 2, . ..,..., k- 1) и если , то i -му члену моделируемого ряда присваивается значение . Затем проверяется i = n , и если равенство выполняется, т. е. получены все п значений, то розыгрыш прекращается, если нет, то i увеличивается на 1 и весь расчет, начиная со 2-го оператора (см. рис. 9.3), повторяется.

Привести в порядок рисунок

Рис. 9.3. Блок-схема розыгрыша ряда значений дискретной случайной величины.

ВВЕДЕНИЕ

Системой принято называть совокупность элементов, между которыми имеются связи любой природы, и она обладает функцией (назначением), которой нет у составляющих ее элементов. Информационные системы, как правило, представляют собой сложные территориально распределенные системы с большим количеством составляющих элементов, обладающие разветвленной сетевой структурой.

Разработка математических моделей, позволяющих оценить показатели функционирования информационных систем, является сложной и трудоемкой задачей. Для определения характеристик таких систем можно применить метод имитационного моделирования с последующей обработкой результатов эксперимента.

Имитационное моделирование является одной из центральных тем при изучении дисциплин "Моделирование систем" и "Математическое моделирование". Предметом имитационного модели­рования является изучение сложных процессов и систем, подвер­женных, как правило, воздействию случайных факторов, путем проведения экспериментов с их имитационными моделями.

Суть метода проста - имитируется “жизнь” системы при многократном повторении испытаний. При этом моделируются и регистрируются случайно меняющиеся внешние воздействия на систему. Для каждой ситуации по уравнениям модели просчитываются системные показатели. Существующие современные методы математической статистики позволяют ответить на вопрос - а можно ли и, с каким доверием, использовать данные моделирования. Если эти показатели доверия для нас достаточны, мы можем использовать модель для изучения данной системы.

Можно говорить об универсальности имитационного моделирования, поскольку оно применяется для решения теоретических и практических задач анализа больших систем, включая задачи оценки вариантов структуры системы, оценки эффективности различных алгоритмов управления системой, оценки влияния измене­ния различных параметров системы на её поведение. Имитационное моделирование может быть положено также в основу синтеза больших систем, когда требуется создать систему с заданными характеристиками при определённых ограничениях, и которая при этом была бы оп­тимальной согласно выбранным критериям.

Имитационное моделирование является одним из наиболее эффективных средств исследования и проектирования сложных систем, а часто единственным практически реализуемым методом исследования процесса их функционирования.

Целью курсовой работы является изучение студентами методов имитационного моделирования и методов обработки статистических данных на ЭВМ с использованием прикладных программных средств. Приведем возможные темы курсовых работ, позволяющих исследовать сложные системы на основе имитационных моделей.

· Имитационное моделирование в задачах одномерного или плоского раскроя. Сравнение плана раскроя с оптимальным планом, полученным методами линейного целочисленного программирования.

· Транспортные модели и их варианты. Сравнение плана перевозок, полученного методом имитационного моделирования, с оптимальным планом, полученным методом потенциалов.

· Применение метода имитационного моделирования к решению оптимизационных задач на графах.

· Определение объемов производства как задача многокритериальной оптимизации. Использование метода имитационного моделирования для нахождения множества достижимости и множества Парето.

· Метод имитационного моделирования в задачах календарного планирования. Получение рекомендаций по составлению рационального расписания.

· Исследование характеристик информационных систем и каналов связи как систем массового обслуживания методом имитационного моделирования.

· Построение имитационных моделей при организации запросов в базах данных.

· Применение метода имитационного моделирования для решения задачи управления запасами с постоянным, переменным и случайным спросом.

· Исследование работы цеха рубительных машин методом имитационного моделирования.

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

Техническая система S состоит из трех элементов, схема соединения которых приведена на рис.1. Времена безотказной работы X 1 , X 2 , X 3 элементов системы являются непрерывными случайными величинами с известными законами распределения вероятностей. Внешняя среда E оказывает воздействие на работу систему в виде случайной величины V с известным дискретным распределением вероятностей.

Требуется оценить надежность системы S методом имитационного моделирования на ЭВМ с последующей обработкой результатов эксперимента. Ниже приводится последовательность выполнения работы.

1. Разработка алгоритмов разыгрывания случайных величин X 1 , X 2 , X 3 и V с использованием генераторов случайных чисел, содержащихся в математических пакетах, например, в Microsoft Excel или в StatGraphics.

2. Определение времени безотказной работы системы Y в зависимости от времен безотказной работы X 1 , X 2 , X 3 элементов на основе структурной схемы расчета надежности.

3. Определение времени безотказной работы системы с учетом влияния внешней среды в соответствии с формулой Z=Y/(1+0,1V).

4. Построение моделирующего алгоритма, имитирующего работу системы S и учитывающего возможность отказа элементов и случайные воздействия внешней среды E. Реализация полученного алгоритма на ЭВМ и создание файла со значениями случайных величин X 1 , X 2 , X 3 , V, Y и Z. Число опытов для машинного эксперимента принять равным 100.

5. Статистическая обработка полученных результатов. С этой целью необходимо

Данные для случайной величины Z разбить на 10 групп и сформировать статистический ряд, содержащий границы и середины частичных интервалов, соответствующие частоты, относительные частоты, накопленные частоты и накопленные относительные частоты;

Для величины Z построить полигон и кумуляту частот, построить гистограмму по плотностям относительных частот;

Для величин X 1 , X 2 , X 3 , V установить их соответствие заданным законам распределения, используя критерий c 2 ;

Для случайной величины Z рассмотреть три непрерывных распределения (равномерное, нормальное, гамма), изобразить на гистограмме для Z плотности этих распределений;

С помощью критерия c 2 выполнить проверку справедливости гипотезы о соответствии статистических данных выбранным распределениям, уровень значимости при подборе подходящего распределения принять равным 0.05.

6. Записать функцию плотности распределения времени безотказной работы Z системы, определить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Z. Определить основные характеристики надежности системы: среднюю наработку до отказа T 1 и вероятность безотказной работы P(t) в течение времени t. Найти вероятность, что система не откажет за время T 1 .

Варианты заданий выдаются из табл.1 индивидуально каждому студенту. Обозначения случайных величин содержатся по тексту в п.2 и 3. Структурные схемы расчета надежности в соответствии с их номерами приведены на рис.1.

Таблица 1

Варианты заданий

Вариант	X 1	X 2	X 3	V	Номер схемы
	LN(1,5;2)	LN(1,5;2)	E(2;0,1)	B(5;0,7)
	U(18;30)	U(18;30)	N(30;5)	G(0,6)
	W(1,5;20)	W(1,5;20)	U(10;20)	П(2)
	Exp(0,1)	Exp(0,1)	W(2;13)	B(4;0,6)
	N(18;2)	N(18;2)	Exp(0,05)	G(0,7)
	E(3;0,2)	E(3;0,2)	LN(2;0,5)	П(0,8)
	W(2,1;24)	W(2,1;24)	E(3;0,25)	B(3;0,5)
	Exp(0,03)	Exp(0,03)	N(30;0,4)	G(0,8)
	U(12;14)	U(12;14)	W(1,8;22)	П(3,1)
	N(13;3)	N(13;3)	W(2;18)	B(4;0,4)
	LN(2;1)	LN(2;1)	Exp(0,04)	G(0,9)
	E(2;0,1)	E(2;0,1)	LN(1;2)	П (4,8)
	W(1,4;20)	W(1,4;20)	U(30;50)	B(3;0,2)
	Exp(0,08)	Exp(0,08)	LN(2;1,5)	G(0,3)
	U(25;30)	U(25;30)	N(30;1,7)	П(2,8)
	N(17;4)	N(17;4)	E(2;0,04)	B(2;0,3)
	LN(3;0,4)	LN(3;0,4)	Exp(0,02)	G(0,4)
	E(2;0,15)	E(2;0,15)	W(2,3;24)	П(1,6)
	W(2,3;25)	W(2,3;25)	U(34;40)	B(4;0,9)
	Exp(0,02)	Exp(0,02)	LN(3,2;1)	G(0,7)
	U(15;22)	U(15;22)	N(19;2,2)	П(0,5)
	N(15;1)	N(15;1)	E(3;0,08)	B(4;0,6)
	LN(2;0,3)	LN(2;0,3)	Exp(0,02)	G(0,5)
	E(3;0,5)	E(3;0,5)	W(3;2)	П(3,6)
	W(1,7;19)	W(1,7;19)	U(15;20)	B(5;0,7)
	Exp(0,06)	Exp(0,06)	LN(2;1,6)	G(0,2)
	U(15;17)	U(15;17)	N(12;4)	П(4,5)
	N(29;2)	N(29;2)	E(2;0,07)	B(2;0,7)
	LN(1,5;1)	LN(1,5;1)	Exp(0,08)	G(0,7)
	E(2;0,09)	E(2;0,09)	W(2,4;25)	П(2,9)

На рис.1 имеется три вида соединения элементов: последовательное, параллельное (постоянно включенный резерв) и резервирование замещением.

Время до отказа системы, состоящей из последовательно соединенных элементов, равно наименьшему из времен до отказа элементов. Время до отказа системы с постоянно включенным резервом равно наибольшему из времен до отказа элементов. Время до отказа системы с резервом замещением, равно сумме времен до отказа элементов.

Схема 1. Схема 2.

Схема 3. Схема 4.

Схема 5. Схема 6.
Схема 7. Схема 8.